Géométrie d'un avion - Définitions et vocabulaire associés
Voyons maintenant plus en détail chaque élément majeur d'un avion de conception classique. Nous verrons en même temps certaines définitions associées.
Comme nous l'avons vu, l'avion est composé :
d'un fuselage,
d'une aile,
d'empennages (un horizontal et un vertical),
etc.
Nous allons commencer par l'aile de l'avion, élément important pour voler, n'est-ce pas ?
Nous verrons ensuite que l'on trouve sur celle-ci, comme sur les empennages, des gouvernes qui permettent au pilote de diriger l'avion.
Nous aborderons ensuite les empennages d'un avion, qui ne sont que de "petites ailes" !
Et pour terminer, nous dirons un mot sur le train d'atterrissage et le fuselage.
L'aile !
Aile, demi-aile ou voilure ?
Avant de commencer, voici une petite question : Pour qu'un avion vole, doit-il avoir une ou deux ailes ? autrement dit, que désigne-t-on par aile?
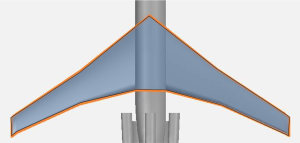
En aéronautique, lorsque nous parlons de l'aile, nous évoquons en général la voilure principale de l'avion, c'est à dire, comme illustré sur le schéma ci-dessous, l'ensemble constitué des parties droite et gauche de l'aile.
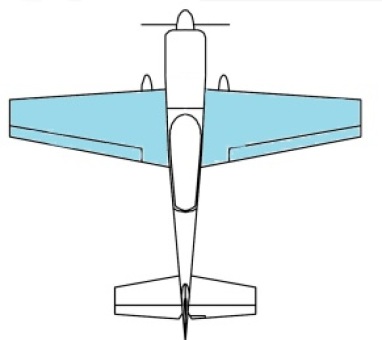
Les différentes zones de l'aile
Commençons par présenter les différentes parties de l'aile pour continuer sur le vocabulaire permettant de définir sa forme géométrique.
Nous pouvons trouver plusieurs zones sur une aile qui ont chacune quelques particularités :
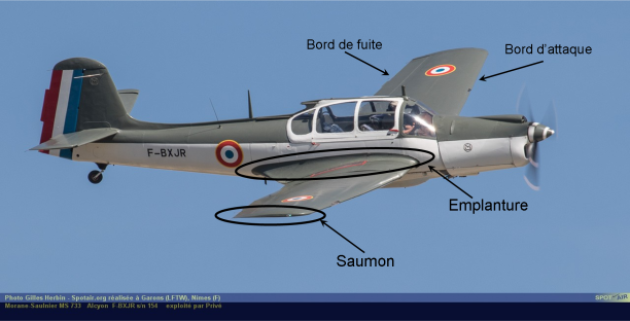
le bord d'attaque ("BA") : c'est la partie de l'aile située à l'avant (quand l'avion est en vol, c'est là où l'air "attaque" l'aile en premier),
le bord de fuite ("BF") : c'est la partie arrière de l'aile (quand l'avion vole, c'est là où, après avoir fini de contourner l'aile, l'air la "quitte"),
l'emplanture de l'aile : c'est la zone de jonction entre l'aile et le fuselage,
le saumon de l'aile : c'est l'extrémité de celle-ci (et cela ne se mange pas !),
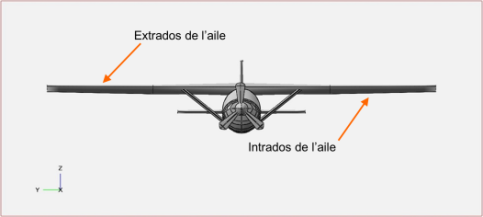
l'extrados : c'est la partie du revêtement qui se situe sur le dessus de l'aile,
l'intrados : c'est la partie du revêtement qui se situe en dessous de l'aile.
Les images ci-dessous illustrent ces différentes zones de l'aile.
La forme géométrique de la voilure
La voilure est un objet géométrique en 3 dimensions plus ou moins complexe. Afin de pouvoir définir l'aile précisément, nous verrons l'aile dans un 1er temps, uniquement en 2 dimensions, comme une projection de l'aile sur une surface plane pour observer sa forme : C'est la forme en plan de l'aile.
Nous utiliserons le vocabulaire suivant pour définir cette forme en plan :
L'envergure,
La corde,
la surface de référence
La flèche,
L'allongement
L'effilement (ou Taper Ratio en anglais)
Toujours en 2 dimensions, nous changerons de point de vue, avec une vue de coté, pour regarder "l'épaisseur de l'aile" avec la description du profil aérodynamique de l'aile.
Enfin nous verrons aussi
Le dièdre,
Toutes ces notions ne sont pas indépendantes les unes des autres. Nous allons y revenir dans la partie "complément" avec quelques formules.
La définition géométrique de l'aile
La forme en plan de l'aile
C'est ce que l'on voit lorsqu'on regarde l'aile du dessus. L'image suivante illustre cette perspective :
Voyons le vocabulaire permettant de décrire la forme en plan de l'aile.
Définition : L'envergure
L'envergure est la distance entre les 2 extrémités (ou saumons) de la voilure.
Nous la noterons très souvent b ou B.
Définition : La corde
On désigne par corde : la ligne droite (toujours parallèle à l'axe longitudinal de l'avion) reliant le bord d'attaque et le bord de fuite de l'aile, ce qui correspond aussi à la distance entre ces deux bords.
Illustration
L'image ci-dessous représente l'envergure b et un exemple de cordes de notre aile.
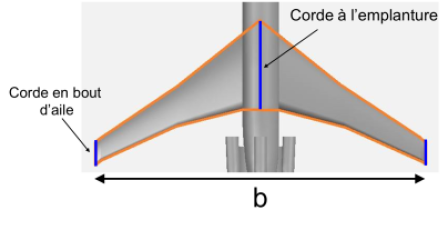
« « Excusez-nous, mais vous parlez de LA corde dans la définition alors que le schéma en montre 2. En plus, nous voyons bien que la corde varie avec sa position ! » »
Vous avez tout à fait raison ! Si nous excluons les ailes en forme de rectangle ou de parallélogramme, alors effectivement la corde varie en fonction de sa position.
S'il est possible de trouver des ailes de forme complexes (elliptique par exemple comme pour le Spitfire - voir image ci-dessous), la plupart des voilures sont trapézoïdales (voir la voilure de l'avion Mudry ci-dessous) ou constituées d'un assemblage de trapèzes (voir le schéma ci-dessous).
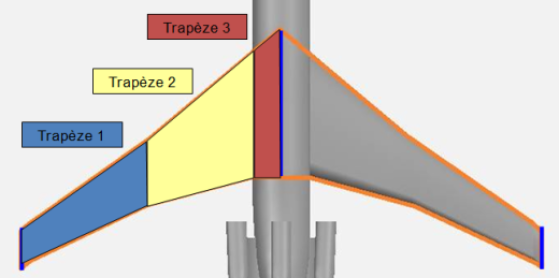
Nous nous intéresserons donc surtout dans ce cours aux ailes trapézoïdales, pour lesquelles, on choisit deux cordes caractéristiques :
la corde au saumon (bout d'aile)
la corde à l'emplanture
Ces deux cordes situées aux extrémités de notre "demi-aile" nous seront utiles pour calculer d'autres paramètres comme la corde géométrique moyenne (CGM) de ce type de voilure.
« Nous avons l'impression que vous utilisez "emplanture" pour désigner 2 choses différentes ! ? »
Attention : Emplanture de l'aile et Corde à l'emplanture ?
Si vous regardez bien le dessin ci-dessus, vous remarquez que la corde à l'emplanture se trouve au milieu de l'aile (axe de symétrie de l'avion).
Vous allez me dire : « Je ne comprends pas ! la corde n'est pas à l'emplanture de l'aile, c'est-à-dire à la liaison entre le fuselage et l'aile, comme vous nous l'avez indiqué juste avant ! ! ? ? ! ! ? ? »
Effectivement, vous avez raison. Ce sont bien deux choses différentes et il y a ici un "abus" de langage :
il y a l'emplanture de l'aile qui est la zone de jonction entre l'aile et le fuselage, et
la corde à l'emplanture qui est bien située au milieu de la voilure (et du fuselage).
Ceci permet par exemple aux concepteurs d'avion de faire varier le diamètre du fuselage sans avoir de conséquence sur la forme de l'aile.
Il faut bien faire attention aux termes utilisés.
Cette différence précisée, voyons maintenant les autres paramètres géométriques de l'aile, en commençant par la définition de la corde géométrique moyenne (CGM) d'une aile non rectangulaire.
Définition : Corde géométrique moyenne
La corde moyenne géométrique CGMcorrespond à la corde d'une aile rectangulaire qui aurait la même surface et la même envergure b que l'aile réelle trapézoïdale considérée.
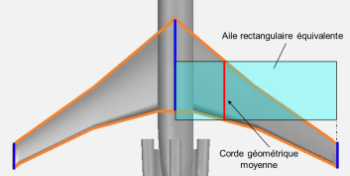
Comme nous l'avons vu, la corde géométrique moyenne permet d'établir une "équivalence géométrique" entre une aile de forme complexe et une aile de forme rectangulaire. Nous verrons par la suite qu'il est intéressant de définir une autre corde : la corde aérodynamique moyenne (CAM) que nous verrons plus tard les compléments.
En attendant, continuons de présenter les différents paramètres géométriques de la forme en plan de notre aile.
Définition : Surface alaire ou surface de référence
La surface de la voilure est la surface correspondant à la projection de l'aile sur un plan horizontal.
C'est en fait - si vous me permettez la comparaison - l'ombre de la voilure de l'avion au sol lorsque le soleil est au zénith (à la vertical de l'avion).
Illustration de la surface alaire
Voici de façon humoristique l'illustration de la projection de la voilure de cet avion (Let 410) au sol.
La faune locale a bien compris la surface alaire "utilisable" de l'avion...
Si nous regardons plus sérieusement, la surface alaire ou de référence, notée S, représente ici la surface plane délimitée en orange. Elle est utilisée pour les calculs de forces aérodynamiques.
Attention : cela comprend aussi la partie du fuselage !
Exemple : Quelques exemples de surface alaire pour les avions
Avion d'aéroclub type DR400 : 14 m²
A320 : 122 m²
surface d'un terrain de basket : 420 m²
A380 : 845 m² (soit 2 fois la surface d'un terrain de basket !)
ATR 72 : 61 m²
Faisons un point, nous avons vue la définition de l'envergure appelée b, de la corde (rappelez-vous qu'il en existe plusieurs, dont la CGM) et la surface alaire (appelée aussi surface de référence).
Voyons maintenant l'allongement où notre corde CGM va nous être utile.
Définition : L'allongement
L'allongement (Aspect Ratio AR en anglais) correspond à l'envergure b divisée par la corde géométrique moyenne (CGM). Il est noté λ.
ainsi, par définition,\(\lambda = \dfrac{b}{C_{GM}}\)
Bien souvent, les caractéristiques techniques publiées d'un avion ne donnent pas la CGM, par contre il est facile de connaître l'envergure et la Surface alaire avec lesquelles il est aussi possible de calculer l'allongement. En effet, en reprenant la définition de CGM et en la combinant à celle de \(\lambda \), nous obtenons :
\(\lambda = \frac{b^2}{S}\)
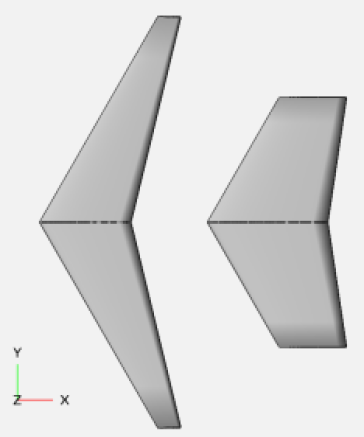
L'allongement donne une idée de l'aspect général de la voilure. Pour une même surface alaire, l'aile peut être plus ou moins allongée.
Les deux ailes présentées ci-dessous ont la même surface mais un allongement différent :
avion de gauche : \(\lambda = 3,6\)et
avion de droite : \(\lambda = 1,33\)
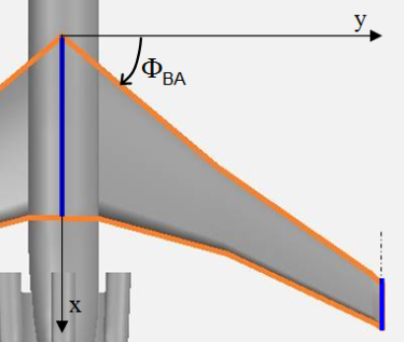
Définition : La flèche d'une aile
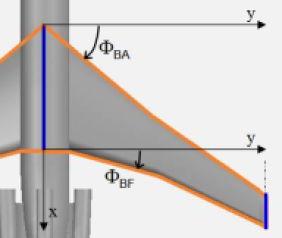
La flèche de l'aile est l'angle φ BA présenté dans la figure ci-dessous.
Quand l'aile est en arrière, dans ce cas, on dit que la flèche est positive. Par contre, quand elle est orientée vers l'avant, on dit que la flèche est inversée ou négative. Le X-29 est un exemple d'avion à flèche inversée :
Attention : Il existe différentes flèches pour une même aile !
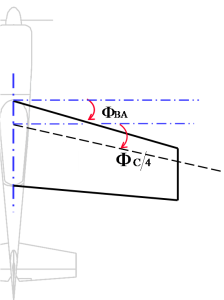
Si au lieu de considérer le bord d'attaque de l'aile, nous considérons par exemple son bord de fuite (comme sur la figure ci-dessous). Nous voyons que l'angle φBF est différent de φBA.
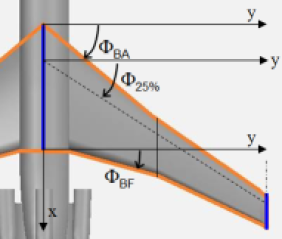
Si maintenant nous considérons la droite reliant tous les points situés à 25% de la corde en partant du bord d'attaque, alors nous obtenons encore une nouvelle flèche !
Il existe une relation mathématique entre la flèche au bord d'attaque et la flèche à 25% de la corde que nous verrons dans les compléments
Remarque : Flèche variable ou aile à géométrie variable
Il existe des avions avec une aile pouvant "être modifiée" pendant le vol. Nous appelons cela une aile à géométrie variable. Ainsi la flèche de cet avion peut varier selon la phase de vol : si l'avion vole à très grande vitesse il "repliera" ses ailes pour obtenir une très grande flèche (voir le dessin de l'aile en pointillé), alors qu'à faible vitesse, il "déploiera" ses ailes , donc aura une flèche plus petite. - un peu comme les oiseaux non ?
Voyons enfin une dernière définition.
Définition : Effilement
L'effilement correspond rapport des cordes aux extrémités de la demi-aile (corde au saumon sur la corde à l'emplanture) :
\(E_{ff}=\frac{C_{saumon}}{C_{emplanture}}\)
En général, la valeur de l'effilement est inférieur à 1. En effet la corde au saumon des avions est plus petite que la corde à l'emplanture, n'est-ce pas ?
Il n'existe que très peu d'avion avec un effilement supérieur à 1. C'est le cas, par exemple, du prototype américain XF-91 :
Exemple : Calcul de l'effilement
Prenons par exemple un avion moyen courrier bi-réacteur type Airbus A320 ou Boeing 737 dont la corde à l'emplanture serait par exemple de 6 mètres et celle au saumon de 1,40 m.
calcul de l'effilement :\(E_{ff}=\dfrac{C_{saumon}}{C_{emplanture}}= \dfrac{1,40}{6}=0,23\)
L'effilement de cet avion est donc de 0,23.
Les compléments !
Au niveau des définitions générales, nous avons vu l'existence de plusieurs cordes dont la Corde géométrique moyenne (CGM) permettant de calculer l'allongement (λ ). La corde aérodynamique moyenne (CAM ) est une autre corde, mais elle est souvent utilisée comme corde de référence pour les calculs aérodynamiques. Voyons sa définition et comment la calculer.
Définition : Corde Aérodynamique Moyenne (CAM)
La corde aérodynamique moyenne (Mean Aerodynamic Chord (MAC) en anglais) correspond à la corde d'une aile rectangulaire de même envergure donnant les mêmes caractéristiques, au niveau du moment de tangage, que l'aile réelle considérée.
« µ$^ù*¨ù^$*ù^$ù%µ^ ! !§ ! Vous parlez de moment de tangage... mais qu'est-ce que c'est ? »
Vous avez raison. Pour le tangage, nous présenterons les axes autour desquels l'avion tourne[8] en fin de chapitre, quand nous abordons la question des gouvernes.
Pour le "moment", c'est une notion de mécanique que l'on peut illustrer de la manière suivante : "Quand on veut faire tourner un objet autour d'un axe, on applique un moment à cet objet autour de l'axe souhaité". C'est équivalent à la force qu'on applique à un objet quand on veut le déplacer...
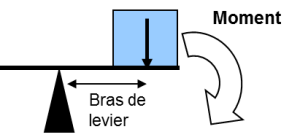
Pour illustrer simplement ce qu'est un moment, considérons le schéma ci-dessous où le cube applique une force (son poids) sur une planche horizontale. Comme la force est appliquée à une certaine distance du point d'appui (cette distance est appelée "bras de levier") on se rend compte que la planche, si elle n'est pas tenue, se met à pivoter autour du point d'appui. Cette rotation montre qu'un moment est appliqué à la planche autour du point d'appui. Ce moment est créé par le poids du cube et il sera d'autant plus grand que le bras de levier ou la force seront grands !
Méthode : Calcul de la corde aérodynamique moyenne
Pour calcul la CAM , il faut appliquer la formule :
\(C_{AM}= \dfrac{2}{3}\times C_{emplanture}\left(\dfrac{1+E_{ff}+E^2_{ff}}{1+E_{ff}}\right)\)
Exemple :
Reprenons notre exemple, avec l'avion A320 ou Boeing 737, où nous avions calculer un effilement de 0,23, et essayons de calculer la CAM .
Calculons de la CAM :
\(C_{AM}= \dfrac{2}{3}\times C_{emplanture}\left(\dfrac{1+E_{ff}+E^2_{ff}}{1+E_{ff}}\right)=\dfrac{2}{3}\times6\left(\dfrac{1+0,23+0,23^2}{1+0,23}\right)=4,17\)
Ainsi la corde aérodynamique moyenne ( CAM ) de ce type d'avion est de 4,17 mètres !
Que faut-il connaître d'autre sur la corde aérodynamique moyenne ?
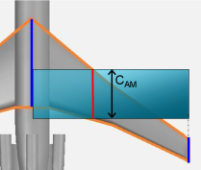
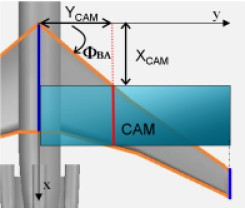
En dehors de sa longueur, il est primordial en aéronautique de connaître sa position sur l'aile, c'est à dire d'une part la distance à laquelle elle se situe de la corde à l'emplanture et d'autre part sa position longitudinale. Il faut donc déterminer les valeurs en et comme illustré sur le schéma ci-dessous.
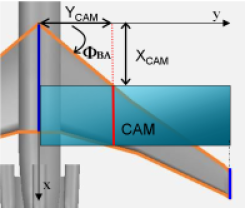
Calcul de la position longitudinale de la CAM
L'angle φBA est la flèche du bord d'attaque de l'aile.
A partir de φBA et de YCAM , il est possible de calculer la longueur xCAM .
Comment ? Et bien avec cette relation :
\(\text{tan φBA}=frac{X}{Y}\)
Méthode : Mais comment trouver la position en envergure de la CAM ?
Et oui, vous avez raison ! C'est bien joli tout cela ! mais il manque une valeur :
nous connaissons la flèche φBA mais nous ne connaissons pas la valeur YCAM ...
Alors comment trouver cette valeur de la position en envergure YCAM ?
Voici la formule à utiliser :
\(Y_{CAM} =\left(\dfrac{b}{6}\right)\dfrac{\left(1+2\cdot E_{ff}\right)}{\left(1+E_{ff}\right)}\)
où est l'envergure de l'aile et
Eff est l'effilement.
Remarque : pour le cas d'un plan vertical d'empennage, la valeur de la position enYCAM (pour l'empennage vertical, ce sera d'ailleurs plutôt ZCAM ...) obtenue avec cette formule doit être multipliée par deux (car l'envergure b d'un empennage vertical correspond déjà à une demi-aile d'avion).
Position en X et Y de la Corde Aérodynamique Moyenne
Relation entre flèche au bord d'attaque et flèche prise au 1/4 de la corde.
Vous connaissez la flèche d'un avion au bord d'attaque, mais vous souhaiteriez connaître celle au 1/4 de la corde... ou inversement. Il existe une relation mathématique entre les deux en fonction de l'effilement et de l'allongement de l'aile. Et oui encore l'effilement et l'allongement, ces paramètres sont à ne pas perdre le bout .... vous suivez le fil ?
Bref, voici la relation qui pourra peut-être vous servir :
\(\text tan \left(\theta_{BA}\right)=\text tan \left(\theta_{C/4}\right)+ \dfrac{1}{\lambda} \dfrac{\left(1-E_{ff}\right)}{\left(1+E_{ff}\right)}\)
Dièdre d'une aile
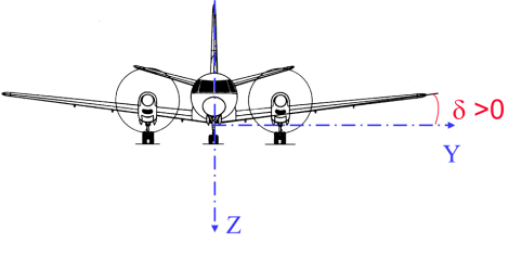
Définition : Dièdre de l'aile
Le dièdre correspond à l'angle entre la perpendiculaire au plan de symétrie de l'avion et la demi-aile vue de face.
Le dièdre se note δ (delta)
il est positif vers le haut (la demi-aile va vers le haut)
Le figure ci-dessus illustre cette définition.
Voici quelques exemples d'avions avec du dièdre
Conclusion sur les termes permettant de définir une aile
Quels sont les termes que nous avons vu sur l'aile :
les contours de l'aile :
bord d'attaque et bord de fuite
extrados et intrados
saumon d'aile et emplanture de l'aile (attention, je rappelle c'est la liaison entre l'aile et le fuselage, ne pas confondre avec la corde à l'emplanture
les définitions de l'aile :
l'envergure
la corde de l'aile et la corde géométrique moyenne (nous avons vu aussi la corde moyenne aérodynamique, l'effilement et l'allongement)
la flèche et le dièdre de l'aile.
et différentes formules permettant de trouver des valeurs de dimensionnement de l'aile en fonction de l'effilement, de l'allongement ou de la flèche par exemple.
Est-ce que ces termes deviennent un peu plus familiers pour vous ?
Oui ? alors on continue ... nous ferons un petit exercice pratique pour vérifier tout cela !
Caractéristiques du profil
Le profil d'aile
Nous avons appris différents éléments de vocabulaire associées à l'aile permettant de définir sa géométrie. Nous allons maintenant aborder quelques termes liés au profil d'une aile.
Si on coupe l'aile par un plan parallèle au plan de symétrie de l'avion, la section a alors une forme très particulière que l'on appelle le profil de l'aile.
Nous retrouvons pour ce profil du vocabulaire déjà vu sur l'aile, comme :
le bord d'attaque, le bord de fuite
l'intrados et l'extrados.
C'est normal, car le profil est une "coupe d'une aile".
D'autres termes sont spécifiques au profil permettant aussi de définir sa géométrie :
La ligne moyenne aussi appelée de cambrure ou de courbure,
la cambrure maximale, la cambrure relative
l'épaisseur maximale, l'épaisseur relative
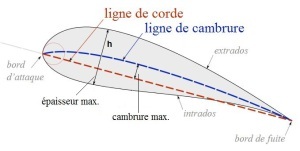
Sur le profil, nous retrouvons donc le bord d'attaque, le bord de fuite, l'extrados, l'intrados, et la corde (ou ligne de corde) : ligne droite joignant le bord d'attaque au bord de fuite.
Exemple : Ordres de grandeur de corde
Boeing 747-400 : 14,63 m à l'emplanture et 4,06 à l'extrémité
Falcon 900 : 4,08 m à l'emplanture et 1,12 à l'extrémité
Airbus 320 : 6,07 m à l'emplanture et 1,49 à l'extrémité
Remarque : Corde : utilisée comme grandeur de référence
La corde du profil de l'aile (ou la corde moyenne) est utilisée comme une longueur de référence pour
indiquer une position le long de la corde (en %)
décrire la forme du profil à l'aide de grandeurs relatives :(grandeurs définies en fonction de la corde, donc exprimées en %)
Pour l'épaisseur du profil, on parlera donc d'épaisseur relative (voir ci-dessous).
L'épaisseur correspond à la distance entre l'intrados et l'extrados (correspondant à h sur le schéma ci-dessus)
Pour la cambrure du profil (ou courbure), on parlera de cambrure relative (voir ci-dessous).
La cambrure d'un profil (ou flèche du profil) correspond à la distance entre la ligne de cambrure et la ligne de corde.
La ligne de cambrure est aussi appelée ligne moyenne car elle est constituée de l'ensemble des points se trouvant à la même distance de l'extrados et de l'intrados. (ligne représentée en bleue sur le schéma ci-dessus)
Épaisseur relative :
L'épaisseur relative (exprimée en %) correspond à l'épaisseur maximale du profil, divisée par la longueur de corde de référence.
\(e=\dfrac{Epaisseur_{max}}{Corde_{Ref.}}=\dfrac{h}{l}=\cdots \text{Exprimé en\% }\)
Prenons l'exemple du Boeing 747-400 :
Sa corde à l'emplanture est de 14,63 m. Et son épaisseur relative pour ce profil est de : 13,4 % . Quelle est alors l'épaisseur maximale de ce profil ?
\(epaisseur_{max}=\dfrac{13,4}{100}\times14,63=1,96 m\)
Et oui ! l'épaisseur maximale de l'aile du Boeing 747-400 au niveau de l'emplanture est de 1,96 mètres.
Cambrure relative ou courbure relative
On appelle la cambrure relative la cambrure maximale (donc la distance maximale entre la ligne moyenne et la corde) divisée par la longueur de la corde (en pourcentage).
\(C=\dfrac{Coubure_{max}}{Corde}= \dots\text{Exprimé en} \%\)
Complément : Pourquoi relative ?
Pourquoi utilise-t-on la notion de grandeur "relative"?
Deux profils avec des dimensions très différentes, auront des comportements aérodynamiques proches, s'ils ont des grandeurs relatives comparables. Cela permet d'étudier des profils de petite échelle en soufflerie semblables aux profils grandeur nature.
L'empennage
Après l'aile qui est l'élément principal pour voler, voyons ensemble une autre partie de l'avion que nous avons déjà évoquée, l'empennage qui est constitué :
du plan ou empennage horizontal qui est similaire à une petite aile avec les mêmes caractéristiques et définitions géométriques,
l'empennage vertical correspondant à une demi-aile.
L'empennage de l'avion Airbus A350 sur la photo correspond à la forme la plus répandue et appelée empennage classique, mais il existe d'autres géométries pour l'empennage.
Voyons les différentes formes que l'on peut rencontrer.
Si le plan horizontal est positionné en haut de la dérive, cela forme un empennage en "T".
Lorsque l'empennage horizontal se trouve cette fois-ci au milieu de la dérive, nous obtenons un empennage appelé "cruciforme médian".
Certains gros avions ont deux dérives formant ainsi un empennage en forme de H.
Enfin, vous verrez parfois des avions sans plan vertical ni plan horizontal....mais avec un empennage en V.
D'un point de vue personnel, je trouve ça très joli mais malheureusement, il est moins efficace dans certaines configurations de vol.
Le train d'atterrissage
Le train d'atterrissage permet à l'avion de rouler au sol, décoller et d'atterrir par ses propres moyens. Il est composé d'un train principal et d'un train auxiliaire. Historiquement, le train auxiliaire était situé à l'arrière du fuselage, au niveau de l'empennage.
Aujourd'hui, il est situé sous le "nez" de l'avion donnant une posture horizontale. De plus, ce train auxiliaire avant est orientable et permet de diriger l'avion au sol.
Il existe donc deux grands types de train d'atterrissage :
le train classique (sur les avions historiques et aujourd'hui sur les avions de voltige)
le train tricycle (que l'on voit maintenant sur tous les avions modernes de transport ou d'aviation général).
Voici un exemple d'avion avec train classique, où vous voyez le train auxiliaire sous l'empennage. Pour les avions légers ce train est bien souvent juste une petite roue libre.
Le train tricycle permet donc d'avoir un avion horizontal au sol, ce qui est plus confortable pour les passagers au moment de l'embarquement, et d'avoir la roue avant directrice lors du roulage.
Le train principal, en fonction du poids de l'avion, peut avoir un nombre plus ou moins grand d'atterrisseurs et de roues. Plus l'avion est lourd et plus le nombre de roues sera important !
Il faut pouvoir répartir toute la masse de l'avion sur ses roues pour que celui-ci n'endommage pas la piste et les parkings des aéroports.
Un avion peut donc avoir aussi plus de deux jambes de train principal. Ces jambes de train s'appellent aussi des atterrisseurs. Par exemple les avions les plus gros peuvent avoir trois jambes de train et même quatre. C'est le cas pour le Boeing 747 et l'Airbus A380 (représenté ci-dessous).
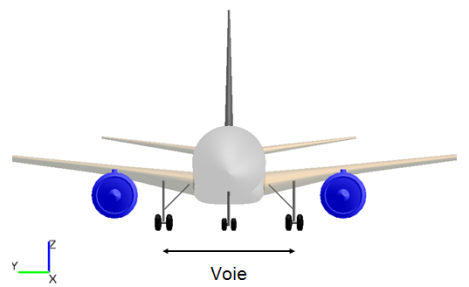
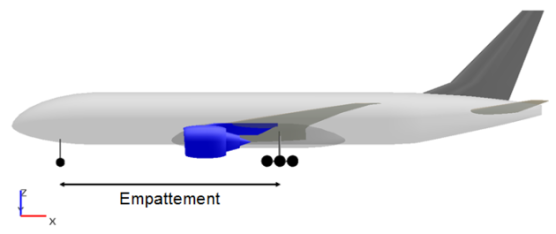
Pour pouvoir se déplacer sur un aéroport, il faut prendre en compte, non seulement, le nombre de roues, mais aussi la géométrie du train d'atterrissage :
l'espacement latéral entre les jambes de train principal (que l'on appelle la voie ou la largeur du train) d'une part et
la distance entre le train auxiliaire et le train principal (que l'on appelle l'empattement) d'autre part.
Si ces dimensions ne sont pas bien définies par le constructeur de l'avion, les compagnies aériennes ne pourront pas l'exploiter sur certains aéroports,ce qui peut poser de gros problèmes !
Ces paramètres sont donc important lors de la conception de l'avion : imaginez un avion très performant en vol mais qui ne peut pas être accueilli sur les aéroports car la largeur de son train d'atterrissage dépasse celle de la piste !
Exemple :
Pour la définition de ses infrastructures, l'aéroport s'intéresse :
aux dimensions de l'avion et en particulier à son envergure et à la largeur de son train d'atterrissage.
Ces éléments sont importants dans la conception des parkings, des pistes ("runways") et des voies d'accès aux pistes ("taxiways").
Ainsi pour aider les exploitants d'aéroport, il existe des documents indiquant toutes les informations (les dimensions, rayons de virages, etc.) nécessaires à l'accueil d'un avion sur une plate-forme aéroportuaire.
Vous voyez bien que le train d'atterrissage est aussi une partie importante de l'avion et qu'il faut notamment :
bien le dimensionner pour supporter le poids de l'avion et sa répartition au sol (nombre d'atterrisseurs et de roues)
bien définir la largeur entre ses atterrisseurs principaux pour la circulation sur les taxiways et les pistes.
Passons maintenant à un sujet différent.
Le fuselage
Le fuselage de l'avion, de forme généralement ronde ou ovale, permet - simplement - la liaison entre les différents éléments de l'avion (aile, empennage, train d'atterrissage, cockpit, moteur). Et oui, sans le fuselage, tous ces éléments seraient au sol ...
Au début de l'aviation, le fuselage ne servait qu'à attacher les empennages arrières et assurait un bras de levier suffisant pour le moment de tangage (vous vous souvenez ?).
Pendant de nombreuses années, la structure des fuselages comprenait une charpente, d'abord en bois, puis en métal.
Effectivement, je suis d'accord avec vous, le rôle principal du fuselage est aussi de transporter des passagers et/ou du fret en plus ou moins grande quantité.
La preuve en est : le Béluga utilisé par Airbus. 
Le fuselage de l'avion est caractérisé par sa longueur et la forme et la dimension de sa section qui est :
souvent ovale ou ronde pour les avions pressurisés volant à haute altitude,
parfois rectangulaire pour les avions non-pressurisés.
Les avions commerciaux ont tous des fuselages de section ovale ou ronde. Mais ils n'ont pas tous le même diamètre ni la même longueur de fuselage.
Nous pouvons regrouper ces avions en fonction de leur diamètre de fuselage, en 2 grandes familles : les avions comme les A320 ou les B737 (que l'on appelle les "narrow body" = fuselage étroit) et les gros avions comme l'A330, le B777 ou encore les B747 et A380 (que l'on appelle les "wide body" = fuselage large).
La longueur du fuselage, elle, dépend bien évidemment de la dimension de l'avion : entre un A380 et un A320, la longueur n'est pas la même !
Mais il y aussi pour une même famille d'avion différentes longueurs de fuselage possibles correspondant à différentes versions. Par exemple, nous verrons qu'entre l'avion A318, A319, A320 et A321, en terme de géométrie, seule la longueur du fuselage change.
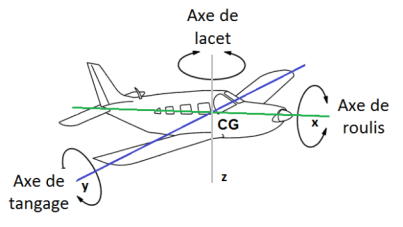
Les trois axes de rotation de l'avion
Le pilote contrôle la position de l'avion autour de 3 axes :
l'axe de roulis (roll en anglais)
l'axe de lacet (yaw)
l'axe de tangage (pitch)
Ces trois axes se coupent en un point : Le centre de gravité (CG) de l'avion.
Le pilote contrôle la position de son avion avec des commandes agissant sur un ensemble de gouvernes associées à chaque axe.
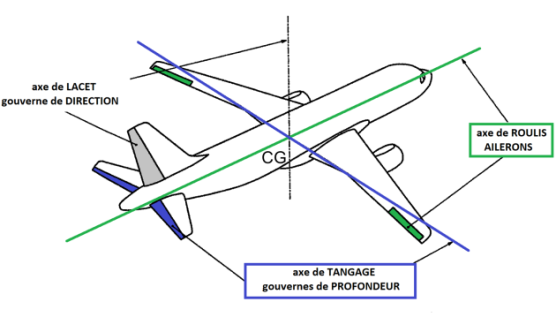
Les gouvernes de l'avion
Afin d'orienter l'avion autour des 3 axes de rotation précédemment décrits, le pilote utilise des surfaces mobiles attachées à l'avion, que l'on appelle les gouvernes (aérodynamiques) de l'avion :
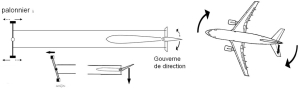
la gouverne de direction (rudder en anglais) pour l'axe de lacet
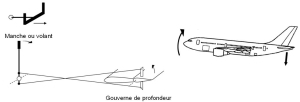
la gouverne de profondeur (elevator) pour l'axe de tangage
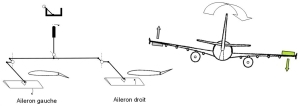
les ailerons (ailerons) pour l'axe de roulis
Les commandes du pilote associées aux gouvernes de l'avion
Pour actionner les gouvernes que nous venons de présenter, le pilote actionne des commandes qui agissent sur ces gouvernes, créant ainsi des forces (et des moments !) qui vont modifier l'équilibre de l'avion et sa trajectoire.
Mouvement en tangage
Le manche ou le volant est tiré en arrière
La gouverne de profondeur se braque vers le haut
L'air a tendance à s'opposer au mouvement de la gouverne
Une force se crée vers le bas sur l'empennage arrière
Le nez de l'avion se lève → mouvement à cabrer
Mouvement en roulis
Le manche est poussé vers la droite
L'aileron droit se lève, et l'aileron gauche se baisse
L'air a tendance à s'opposer au mouvement des gouvernes
Une force se crée vers le bas sur l'aile droite, et vers le haut sur l'aile gauche
L'avion roule vers la droite → mouvement en roulis
Mouvement en lacet
Le pied droit pousse sur la "pédale" de droite
La gouverne de direction se braque vers la droite
L'air a tendance à s'opposer au mouvement de la gouverne
Une force latérale se crée vers la gauche à l'arrière de l'avion
Le nez de l'avion tourne vers la droite → lacet à droite
Airbus A318 - visualisation en 3D - Entraînement
Attention : utilisation d'adobe Flash
Pour utiliser la visualisation de l'Airbus A318 en 3D, il est nécessaire d'avoir l'application Adobe Flash Player !
Nota : pour Regardez l'avion Airbus A318 en 3D sur le site d'Airbus à cette adresse - faites le tourner avec votre souris et entraînez-vous à identifier et nommer les différents éléments de l'avion que nous avons vu dans dans ce chapitre :
par exemple, l'aile, le saumon d'aile, bord d'attaque, les différents axes de rotations et le vocabulaires associés,etc.
l'empennage , avec le plan vertical (dérive et gouverne de direction) et le plan horizontal (plan fixe et gouverne de profondeur) ,
le fuselage...